了解自然混响和数字混响
数字信号处理可以让我们将音乐放置在不同的(虚拟)“空间”中。
作者:Nigel Redmon
编译:PrincessX
这篇文章由EarLevel Engineering提供。
小编注释:这篇文章本来是发表于1997年的,但是时至今日,文中的内容还是很有参考价值。
混响,是录音棚数字信号处理效果中最有趣的方面之一。这是一个非常适合数字信号处理的过程,如果用模拟电子处理的话,会变得很不方便。正因为如此,数字信号处理可以让我们将音乐放置在不同的(虚拟)“空间”中。
在数字处理诞生之前,混响效果都是用换能器创造出来的——基本上就是一个音箱和一个话筒——物理延迟元件的两端。延迟元件也就是一套金属弹簧,一块悬挂的金属板,或者是一个真正的房间。物理延迟元件在对混相声的控制上有着很大的局限。而且这些创造混响“空间”的元件也不是很便于携带;弹簧混响算是唯一比较方便携带的——而且也是比较经济的——选择,但是用金属弹簧创造出的混响从声音质量的角度上来看,是最劣质的。
首先,让我们来看一下什么是混响:自然混响是指声音在某一个空间中通过界面反射所得到的混相声。声音从发声源中以1100英尺每秒的速度向四周发散开去,然后触碰到墙面,并以不同的角度进行反射。有些反射声会立即进入到你的耳朵(“early reflections”前期反射),而另外的一些反射声则会继续被反射到其他的墙面上,直到进入你的耳朵为止。一些比较厚重的界面——比如说水泥墙——对声音的反射可以说基本上是不带衰减的,然而一些比较软的界面,就会相对吸收更多的声音,尤其是声音中的高频段。房间的大小,构造的复杂性和墙面的角度,以及房间中的东西,另外还有反射界面本身的密度,都会影响到一个房间的声音特质。
但是在数字信号处理中,延迟的时间只受可用内存空间、反射次数的限制。而且与频率相关的效果(滤波器)也只收信号处理速度的限制。
两种可行的模拟混响方式
让我们来看一下两种可行的数字混响模拟方式。第一种,简单粗暴型。
混响是一个不随时间改变的声音效果。这意味着当你弹奏一个音符的时候,不会因为时间的变化而影响到混响——你无论如何都会得到一个相同的通道混响效果。(将混响与受时间影响的效果器进行对比,比如说flanging镶边效果,输出的声音会受到音符和镶边扫频之间关系的影响。)
不受时间影响的系统可以完全通过一个简单的脉冲响应来被定性。你是否曾经进入过一个很大的空房间——比如说一个体育馆或者大厅——然后聆听这个房间的声音特性?你可能只是发出了一声很短的声音——比如拍了一下手什么的——然后你就会听到混相声此起彼伏。如果你有注意到过的话,那么你听到的就是房间本身对声音的脉冲响应。
这个脉冲响应可以告诉你关于房间的一切信息。只需要拍一下手,就可以立即知道房间的混响特性,以及混响时间的长短,而且也可以知道房间的声音是否足够“好”。我们不仅可以用肉耳去判断这个房间脉冲响应的特性,同时也可以用先进的信号分析器,对这个房间的混响做出分析。事实上,脉冲响应可以告诉我们一切我们想要知道的信息。
这种方法可行的原因在于:脉冲,从它的理想原型来说,是一个在所有频率段拥有相同能量的瞬态的声音。因此我们得到的,就是房间对这个瞬态全频信号的响应,这种响应就是房间的混响。
(一个脉冲信号以及它的响应)
在现实世界中,拍手——或者气球爆炸,鞭炮爆炸,或者一个电弧的噼啪声——都可以被认定为一个声音脉冲。如果你对房间的声音特性进行数字化,并在一个声音编辑软件中审视它的话,它看上去就像是衰减的噪音。一开始会有一些高密度的能量堆积,之后就会逐渐衰减到零。事实上,如果房间本身的声音特质更圆滑,那么声音衰减也就更圆滑。
在数字信号处理中,你很容易意识到,每次响应的采样点都可以被视为初始脉冲信号的一个离散的回声响应点。因为,从理想状态来看,脉冲信号就是一个非零的声音样本,不难想象,一系列的声音样本——比方说在房间里发出的一个声音——可能是每一个单独声音样本在他们各自存在时间里回声响应的总和(这种现象被称为声音叠加)。
换句话说,如果我们有某个房间的一个数字化的声音脉冲信号特性,我们就可以很容易地把这个特性添加到任何的未经处理的数字干声上。将声音样本的音量和每一个脉冲响应点相乘,就可以得到房间对这个声音样本的响应;我们只需要对每一个我们想要“放进”那个房间的声音进行这个处理就可以了。这样我们只需要将声音样本放在一起,就可以得到很多重叠的响应。
这种方法确实简单,但是我们需要为此付出很多的经费在计算机的处理上。每个输入的声音样本都需要单独与脉冲响应相乘,然后再相加成为最后的输出结果。如果我们n个声音样本需要被处理,假设脉冲响应是m个样本的长度,那么我们就需要进行n+m次相乘和相加。所以,如果房间对声音的脉冲响应是3秒的话(可能是一个大房间),如果我们需要处理一个一分钟的音乐,那么我们就需要进行将近350万亿次乘法运算,以及同样次数的加法运算(假设我们的采样率是44.1kHz)。
如果你可以接受这个事实的话,那么你可以让你的电脑花上一天的时间处理这些数据,然后你可以在第二天听到最终的处理结果,但是这明显不适合我们需要的实施效果处理。这事实上真的太坏了,因为这个过程在很多方面都可以得到提升。尤其是,你其实可以准确地模拟出世界上任何房间的声音特性,只要你有它的脉冲响应的话,而且你也可以很简单地创造出属于你自己的人造脉冲响应,并以此创造出一个属于你自己的“空间”(比如说,一个简单的衰减噪音序列虽然可能很简单,但是却可以带来一个圆滑的混响,而且这种混响也是带有更多个性色彩的)。
事实上,有一个更实用的处理方法。我们刚刚一直在讨论关于时间范围内的处理,将两个采样信号相乘的数字信号处理过程被称为“convolution”(卷积)。和时间领域的卷积处理不同的是,同样的卷积处理在频率范围内则不需要这么多的运算过程,可以大大减少电脑后台的运算量(对时间领域进行卷积处理所需要消耗的运算量是在频率领域进行卷积处理运算量的好几倍)。在此我就不再详述了,但是你可以去看一下Bill Gardner的一篇文章,“Efficient Convolution Without Input / Output Delay”(没有输入/输出延迟的高效卷及处理),或许你可以从中找到更好的处理方法。(我自己还没有尝试过这种技术,但是如果我有时间的话,我也会去尝试一下这种方法的。)
获得数字混响的一个有效途径
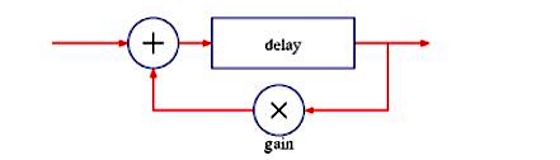
我们众所周知的备受宠爱的数字信号混响可以有很多种不同的方式。基本来说,它们会使用多个信号延迟和信号回馈来创建出一系列高密度的回声,这个回声会随时间渐渐衰减。这其中一些功能性的构造元件大家已经都了解了;然而真正能给一个数字信号混响赋予属于自己的个性声音的重要因素,在于这些构造的变体以及这些构造元件是如何相互合作的。最简单的方式,是创造一个延迟模块,然后再将部分经过延迟后的声音信号再回馈给这个延迟模块,这样就能创造出一个重复的逐渐衰减的回声效果(回馈给延迟信号的声音信号必须小
1)。将不同深度的类似这种延迟效果的声音信号混起来,就可以增加回声的密度,而且混响听起来也更加真实。比如说,用根据质数产生的不同长度的延迟可以确保每一个回声都可以恰好在另外两个回声之间,这样就增强了回声的密度。
但在实战中,这个看似简单的原理却不怎么好用。你需要太多这种硬回声才能创造出一个圆滑的混响墙。而且,使用简单的信号反馈也是梳状滤波器的一个秘方,梳状滤波器可以带来频率抵消,这样就可以模拟出真实的房间效果,但是也可能带来环形调制效果和不稳定的声音。尽管很有用,但是如果只有这些梳状滤波器的话,还是不能给出一个令人满意的混响效果。
(梳状滤波混响单元)
相反,如果在反馈信号的同时,也将一部分信号继续向前推送,我们就可以弥补这些频率抵消,这样的系统就是一个全通滤波器。全通滤波器也可以给我们之前所说的梳状滤波器产生的效果,而且还能达到更加圆滑的频率响应。将这些梳状滤波器和全通环形延迟效果器,以及其他的处理单元(如用于模拟高频吸收的反馈路线中的高频滤波器单元)相结合——不管是串联、并联,还是嵌套式组合——都能得到一个相对令人满意的结果。
(全通滤波器混响单元)
我就说到这里了,因为已经有很多现有的关于这些观点的文章,而且我写这篇文章也只是为了向大家做一个简单的介绍而已。从我个人而言,我从Hal Chamberlin的“Musical Applications of Microprocessors”中得到了很多有用的信息,此外,Bill Gardner对于这些原理的文章也能在这个网页上找到。
Nigel Redmon是一个音乐家、电子软件工程师,以及独立的研发家,致力于数字音频信号处理领域。他参与研发的产品有:Line 6、Equator Audio、Alesis、Oberheim等等。
可下载Midifan for iOS应用在手机或平板上阅读(直接在App Store里搜索Midifan即可找到,或扫描下面的二维码直接下载),在iPad或iPhone上下载并阅读。
转载文章请注明出自 Midifan.com